数据结构与算法 - AST

全文 ≈ 1.8k字   |   预计阅读时长 9分钟

AST（Abstract syntax tree）抽象语法树，用于表示编程语言源代码的一种抽象语法的结构，树的每个节点都对应源代码中的一个结构。

前言

计算机如何生成 AST 结构？一般来说顺序如下：

  1. 词法分析

扫描源代码，生成标记（token）

  1. 语法分析

解析 tokens，构造 AST 结构

分析过程：

AST 结构：

应用场景

AST 应用场景比较广泛，比如：

  • Typescript 编译 Javascript 文件

  • 格式化插件

  • 代码混淆/压缩

  • 类型检查/推导

等等…诸多应用场景。

词法分析

如何读入源代码，扫描、解析以及生成 AST？下面尝试用一个可以计算+、-、*、/公式的小程序来学习和实验。

假设，给定的源码是1+2+3，应该怎样去扫描？扫描原理很简单，通俗的说就是按字符读取记录为 Token。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 首先定义存储标记的结构
type Token struct {
	Str   string
}

// 扫描源码
s := "1+2+3"
tokens := []Token{}
for _, c := range s {
	tokens = append(tokens, Token{
		Str: string(c),
	})
}
fmt.Printf("%+v\n", tokens)
// [{Str:1} {Str:+} {Str:2} {Str:+} {Str:3}]

以上，扫描工作就完成了！

但词法分析一般没有这么简单，比如数字1和操作符+也不应该是同一种类型。所以我们需要改造词法分析器！在生成 Token 的同时记录类型，方便进一步处理。这里我们使用状态机的设计思路：

  1. 读入一个字符
  2. 判断字符类型，数字 or 操作符
        1. 是数字，记录当前字符位置，继续读取下一个字符，直至非数字或者字符边界，记录完整的数值。
        2. 不是数字，直接记录操作符。
  3. 返回 token

详细扫描逻辑，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
type Lexer struct {
	Expression string
	Char    byte
	Pos     int
}

type Token struct {
	Str   string
	Type  int
	Start int
	End   int
}

func (r *Lexer) Lex() ([]*Token, error) {
	tokens := make([]*Token, 0)
	r.Char = r.Expression[0]
	for r.Pos < len(r.Expression) {
		token := r.Scan()
		if token.Type == enums.ILLEGAL {
			return []*Token{}, fmt.Errorf("'%s' is not supported", token.Str)
		}
		tokens = append(tokens, token)
	}
	return tokens, nil
}

func (r *Lexer) Scan() *Token {
	var token *Token
	pos := r.Pos
	switch r.Char {
	case
		'0',
		'1',
		'2',
		'3',
		'4',
		'5',
		'6',
		'7',
		'8',
		'9':
		for r.IsDigit() {
			if !r.NextChar() {
				break
			}
		}
		token = &Token{
			Str:   string(r.Expression[pos:r.Pos]),
			Type:  enums.NUMBER,
			Start: pos,
			End:   r.Pos,
		}
	case '+':
		token = &Token{
			Str:   string(r.Char),
			Type:  enums.ADD,
			Start: pos,
			End:   pos,
		}
		r.NextChar()
	case '-':
		token = &Token{
			Str:   string(r.Char),
			Type:  enums.SUB,
			Start: pos,
			End:   pos,
		}
		r.NextChar()
	case '*':
		token = &Token{
			Str:   string(r.Char),
			Type:  enums.MUL,
			Start: pos,
			End:   pos,
		}
		r.NextChar()
		if r.Char == '*' {
			token = &Token{
				Str:   "**",
				Type:  enums.XOR,
				Start: pos,
				End:   pos,
			}
			r.NextChar()
		}
	case '/':
		token = &Token{
			Str:   string(r.Char),
			Type:  enums.QUO,
			Start: pos,
			End:   pos,
		}
		r.NextChar()
	default:
		token = &Token{
			Str:   string(r.Char),
			Type:  enums.ILLEGAL,
			Start: pos,
			End:   r.Pos,
		}
	}
	return token
}

现在，我们调用词法分析器解析1+2+3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
lexer := lexer.Lexer{
	Expression: "1+2+3",
}
tokens, err := lexer.Lex()
if err != nil {
	fmt.Println(err)
	return
}
for _, token := range tokens {
	fmt.Printf("%+v \n", token)
}
// &{Str:1 Type:9 Start:0 End:0}
// &{Str:+ Type:10 Start:1 End:1}
// &{Str:2 Type:9 Start:2 End:2}
// &{Str:+ Type:10 Start:3 End:3}
// &{Str:3 Type:9 Start:4 End:4}

语法分析

生成 tokens 是第一步，这一串 token 又要怎样去解析呢？

已知+-*/均属于二元运算，二元运算三元素：运算符、左变量、右变量。所以我们需要的结构大概是这样：Number{1} Op{+} Number{2} Op{+} Number{3}，用二叉树来表示：

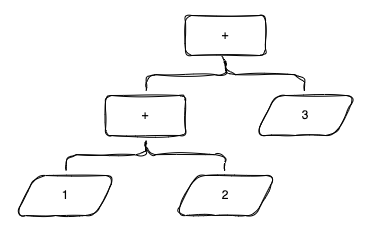
drawing 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 首先定义一个语法分析器
type Parser struct {
	Tokens   []*lexer.Token // tokens
	CurToken *lexer.Token 	// 当前token
	Index      int			// 下标
	Err      error			// error
}

// 数值结构
type Number struct {
	Val int
}

// 二元运算结构
type Stmt struct {
	Type  int
	Left  Node
	Right Node
}

处理逻辑如下：

  1. 顺序取出一个 token。
  2. ParseExpr()判定 token 类型，返回对应结构，下标+1（处理下一个 token，应当是运算符 token）。
        1. 如果是数值类型，则直接返回 Number{}结构。
        2. 如果是运算符类型，则递归处理返回 Stmt{}结构。
  3. ParseRight()处理右侧变量，把左侧变量传入函数。
  4. 根据运算符判断变量优先级问题，如果当前运算符小于传入变量优先级，则直接返回传入变量，处理结束。
  5. 记录当前运算符（类型），下标+1，处理当前操作符右侧变量（步骤 2）。
  6. 再次判断传入变量优先级是否低于当前运算符。
        1. 是，则把右侧变量（步骤 4）当成左侧变量传入递归处理。
        2. 不是，则构造二元运算表达式 Stmt{Type: 运算符类型, Left: 左侧变量, Right: 右侧变量}。
  7. 当前循环结束，回到步骤 4。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
func (r *Parser) Parse() (Node, error) {
	if len(r.Tokens) == 0 {
		return nil, errors.New("the token list is empty")
	}
	if r.CurToken == nil {
		r.CurToken = r.Tokens[0]
	}
	return r.Compile(), r.Err
}

func (r *Parser) Compile() Node {
	left := r.ParseExpr()
	right := r.ParseRight(1, left)
	return right
}

func (r *Parser) ParseExpr() Node {
	switch r.CurToken.Type {
	case enums.NUMBER:
		return r.ParseNumber()
	case enums.ADD:
		return r.ParseNumber()
	case enums.SUB:
		if t := r.NextToken(); t.Type == enums.EOF {
			r.Err = errors.New("expects to be number, eof given")
			return nil
		}
		return &Stmt{
			Type:  enums.SUB,
			Left:  &Number{},
			Right: r.ParseExpr(),
		}
	case enums.MUL:
		return r.ParseNumber()
	case enums.QUO:
		return r.ParseNumber()
	default:
		r.Err = fmt.Errorf("expects to be number, '%s' given", r.CurToken.Str)
		return nil
	}
}

func (r *Parser) ParseRight(precedence int, left Node) Node {
	for {
		curPrec := r.Precedence()
		if curPrec < precedence {
			return left
		}
		tokenType := r.CurToken.Type
		r.NextToken()
		right := r.ParseExpr()
		if right == nil {
			return nil
		}
		if curPrec < r.Precedence() {
			right = r.ParseRight(curPrec, right)
			if right == nil {
				return nil
			}
		}
		left = &Stmt{
			Type:  tokenType,
			Left:  left,
			Right: right,
		}
	}
}

func (r *Parser) ParseNumber() *Number {
	f, err := strconv.ParseFloat(r.CurToken.Str, 64)
	if err != nil {
		return &Number{}
	}
	node := &Number{
		Val: f,
	}
	r.NextToken()
	return node
}

func (r *Parser) Precedence() int {
	switch r.CurToken.Type {
	case enums.ADD, enums.SUB:
		return 1
	case enums.MUL, enums.QUO:
		return 2
	default:
		return 0
	}
}

看看效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
lexer := lexer.Lexer{
	Expression: "1+2-3*4",
}
tokens, err := lexer.Lex()
if err != nil {
	fmt.Println(err)
	return
}
p := &parser.Parser{
	Tokens: tokens,
}
ast, err := p.Parse()
if err != nil {
	fmt.Println(err)
	return
}
fmt.Printf("%+v \n", ast)
// {Type: 10, Left: {Type: 10, Left: {Type: 9, Val: 1}, Right: {Type: 9, Val: 2}}, Right: {Type: 9, Val: 3}}

最后

有了 AST 结构，我们就可以开始进行计算啦～这样一个支持+-*/的小程序就完成了！计算逻辑相对比较简单，这里直接贴代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 数值类型
func (r *Number) Evaluate() float64 {
	return r.Val
}

// 二元运算类型
func (r *Stmt) Evaluate() float64 {
	left := r.Left.Evaluate()
	right := r.Right.Evaluate()
	switch r.Type {
	case enums.ADD:
		return left + right
	case enums.SUB:
		return left - right
	case enums.MUL:
		return left * right
	case enums.QUO:
		if right == 0 {
			fmt.Printf("expr[%g/%g]exception, division by zero \n", left, right)
			return 0
		}
		return left / right
	default:
		return 0
	}
}

附上完整代码：math-evaluate

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

性格内向安静腼腆的<br />小屁屁